Howdy, folks. As Jeremy has mentioned, this past Friday, April 4th, we hosted a webinar to demonstrate Isograph's FaultTree+ tool. One of the topics we discussed was how you can use the Fault Tree and Event Tree features of the tool to perform a quantitative Layer Of Protection Analysis (LOPA). This post will serve as a little summary of that meeting, for anyone who was unable to attend.
The first stage of a LOPA might be done externally to a quantitative tool like Fault Tree. The first thing you'd want to do is identify hazards, determine an acceptable risk level for those hazards, and ask what you're doing to mitigate them. This might have more in common with a Hazop study. Once you've identified your hazards and protection layers against those hazards, the next thing you might want to do is quantify it. How often will the hazard occur? How effectively will our layers of protection mitigate the risk of the hazards? Can we objectively rank these risks? This sounds like a job for Fault Tree and Event Tree analysis.
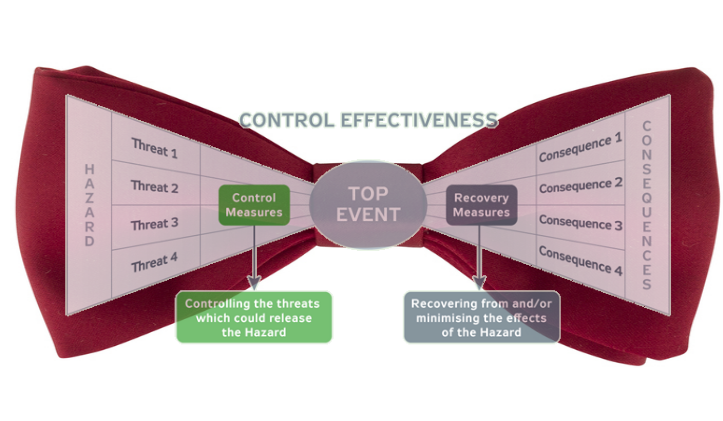
A Fault Tree can very easily be used to quantify a hazard. In fact, that's the primary usage of the method. By coupling it with an Event Tree, we can find out how well that hazard is mitigated by protection systems. If you're not familiar with it, Event Tree analysis is related to Fault Tree analysis. It uses a similar quantitative calculation. The difference is that, while Fault Trees examine the failure leading to a hazard, Event Trees examine the consequences following the hazard. Sometimes, when coupled together, they're called "bowtie events".
Let's look at an example. Suppose that we determine through Fault Tree analysis that the frequency of a fire occurring in a particular system is 0.2 per year, or about one every five years. Now, there are two fire protection systems designed to mitigate the risk of the fire. If both operate, then no severe safety consequences will arise from the fire. However, if one or the other or both protections systems fail, then potentially severe consequences can occur.
Event Tree analysis can easily model this scenario. The Fire is the initiating event, and the layers of protection make up the enabling events. Each branch in the Event Tree represents the success or failure of one of the protection systems. The branches terminate in a consequence, which represents the number of fatalities that might occur from the sequence of events. In this particular example, the "Primary Fire Protection System" is represented by a Fault Tree, and the "Secondary Fire Protection" has been reduced to a single basic event.
When Reliability Workbench analyzes this tree, it applies AND logic at each branch, multiplying the probabilities of the protection system, to obtain a frequency of occurrence for each consequence. These consequences may be assigned a weight, which is multiplied by frequency to obtain a risk. Summing the risks of each consequence tells us, basically, how many deaths might occur per year due to the fire hazard.

Traditional LOPA demands that the layers of protection be independent of one another. That is, the occurrence or failure of one layer must not affect the likelihood of failure in another layer. This is because of the simplistic method of evaluating the layers of protection, where simple AND logic is applied at each branch, as we have seen. Our Fire Event Tree meets this requirement, but in practical examples, this is not necessarily the case. Sometimes layers will share a common element, like a sensor or power. This would make the multiplication of probabilities at each branch an inaccurate—and optimistic—method of evaluating the risk.
The advantage to Fault Tree and Event Tree analysis combined is that the Boolean algebra method used to evaluate cut sets can account for these dependencies between layers of protection. By resolving the Fault Tree and Event Tree combinations to individual basic events, we can correctly account for dependencies. Let's look at a more complex example.
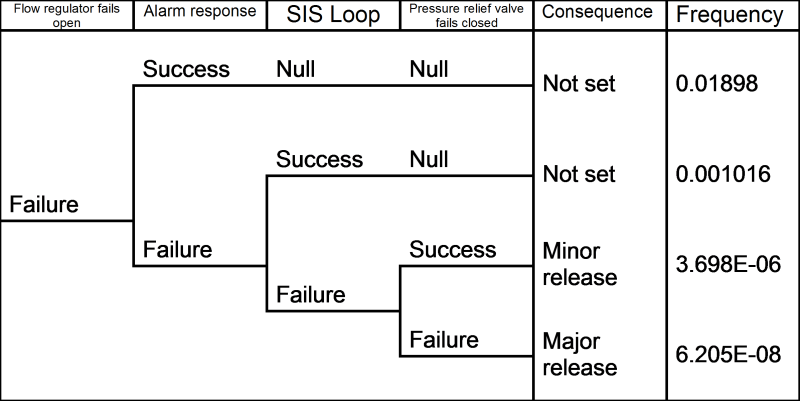
In this case, a chemical is pumped into a reactor vessel. If the flow regulator that admits the liquid to the vessel fails open, it will lead to an increase in pressure that could potentially rupture the vessel and cause a chemical spill. To mitigate this risk, there are two protection systems designed to halt the reactor process in the event of a pressure or temperature build-up: a manual alarm response and an automatic safety-instrumented system. In the event that both these layers fail, there is the additional protection of a pressure relief valve that can vent some of the pressure.
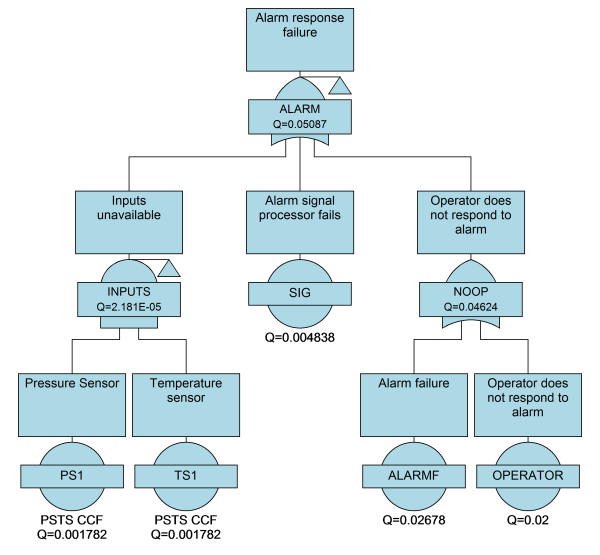
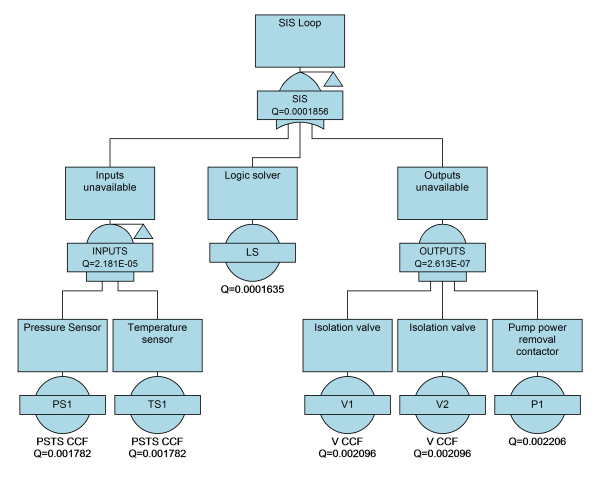
Now, in this example, both the manual alarm response and the SIS loop have common elements: they both depend upon a pressure and temperature sensor to tell them when a hazardous condition arises. Should these inputs fail, then neither protection layer would be able to operate.
Using Fault Tree and Event Tree analysis, we can model this scenario by solving for the cut sets of each path through the event tree. The Boolean logic here will take into account that if the sensors are unavailable, it will affect both manual and automatic shutdown systems.
Once we have analyzed our layers of protection, we can compare the current risk level to what we have defined as an acceptable level. If we're exceeding the risk threshold, then we can quantify how much more risk reduction is required to meet our safety requirements. The importance analysis feature in Reliability Workbench can be used to help find weak points that would benefit most from improvement, but that's a topic for another post.